"Millennium Prize Problems" ialah tujuh masalah matematik terkenal yang dipilih oleh Clay Mathematics Institute pada tahun 2000. Lebih menarik lagi, pihak Clay Mathematics Institut telah menjanjikan hadiah AS$1 juta untuk penyelesaian yang betul bagi mana-mana masalah ini.
Oleh itu, sejumlah $7 juta merupakan hadiah yang ditawarkan sekiranya anda berjaya menjawab kesemua 7 soalan matematik tahap tinggi ini. Sehingga kini, satu-satunya masalah "Millennium Prize Problems" yang telah diselesaikan ialah soalan berkaitan "Konjektur Poincaré".
BESARKAN TEKS A- A+
Clay Mathematics Institut menganugerahkan hadiah wang hadiah mereka kepada ahli matematik Rusia Grigori Perelman pada tahun 2010. Bagaimanapun, beliau menolak anugerah itu kerana hadiah serupa tidak turut ditawarkan kepada Richard S. Hamilton yang mana sebahagian hasil jawapannya diguna oleh Grigori Perelman untuk menyelesaikan soalan berkaitan "Konjektur Poincaré" ini.
6 lagi soalan yang masih belum dapat diselesaikan sehingga ke hai ini adalah "Konjektur Birch and Swinnerton-Dyer", "Konjektur Hodge", "Persamaan Navier-Stokes", "P vs NP", "Hipotesis Riemann" dan juga "Teori Kuantum Yang–Mills".
1. Konjektur Poincaré
Dalam bidang matematik topologi geometri, konjektur atau tekaan Poincaré ialah teorem tentang pencirian 3-sfera, yang merupakan hipersfera yang membatasi unit bola dalam ruang empat dimensi.
Pada asalnya diandaikan oleh Henri Poincaré pada tahun 1904, teorem berkenaan ruang yang kelihatan seperti ruang tiga dimensi biasa tetapi takatnya terhad. Percubaan untuk menyelesaikan teorem ini memacu banyak kemajuan dalam bidang topologi geometri pada abad ke-20.
2. Konjektur Birch dan Swinnerton-Dyer
Dalam tahun-tahun kebelakangan ini, ahli algebra telah mengkaji secara khusus lengkung eliptik, yang ditakrifkan oleh jenis persamaan diophantine tertentu. Lengkung ini mempunyai aplikasi penting dalam teori nombor dan kriptografi, dan mencari penyelesaian nombor bulat atau rasional kepada mereka adalah bidang kajian utama.
Konjektur Birch dan Swinnerton-Dyer memperkatakan jenis persamaan tertentu: yang mentakrifkan lengkung elips ke atas nombor rasional. Tekaanya ialah terdapat cara mudah untuk mengetahui sama ada persamaan tersebut mempunyai bilangan penyelesaian rasional terhingga atau tak terhingga.
3. Konjektur Hodge
Abad ke-20 menyaksikan perkembangan teknik canggih untuk memahami lengkung, permukaan dan permukaan hiper yang merupakan subjek geometri algebra. Bentuk yang sukar dibayangkan boleh dibuat lebih mudah melalui alat pengiraan yang rumit.
Konjektur Hodge mencadangkan bahawa jenis struktur geometri tertentu mempunyai rakan algebra yang sangat berguna yang boleh digunakan untuk mengkaji dan mengelaskan bentuk ini dengan lebih baik.
4. Persamaan Navier-Stokes
Persamaan Navier-Stokes ialah versi dinamik bendalir bagi tiga hukum gerakan Newton. Persamaan ini menerangkan bagaimana aliran cecair atau gas akan berkembang dalam pelbagai keadaan.
Sama seperti undang-undang kedua Newton memberikan penerangan tentang bagaimana halaju objek akan berubah di bawah pengaruh daya luar, persamaan Navier-Stokes menerangkan bagaimana kelajuan aliran bendalir akan berubah di bawah daya dalaman seperti tekanan dan kelikatan, serta daya luaran seperti graviti.
5. P vs NP
Persoalannya ialah sama ada atau tidak, untuk semua masalah yang melibatkan algoritma boleh mengesahkan penyelesaian yang diberikan dengan cepat (iaitu, dalam masa polinomial - P), algoritma juga boleh mencari penyelesaian itu dengan cepat.
Oleh kerana yang pertama menerangkan kelas masalah yang disebut NP, manakala yang kedua menerangkan P, soalannya adalah sama dengan bertanya sama ada semua masalah dalam NP juga dalam P. Ini secara amnya dianggap sebagai salah satu soalan terbuka yang paling penting dalam matematik dan sains komputer.
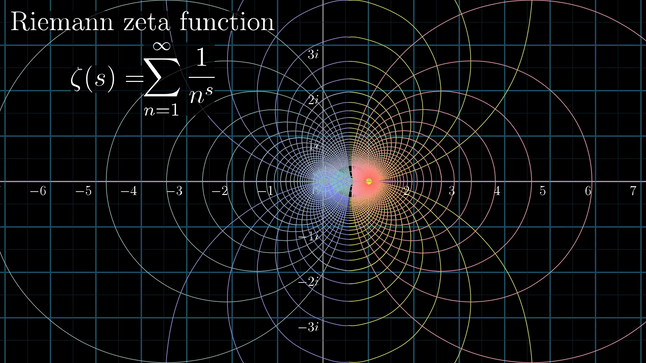
6. Hipotesis Riemann
Dalam matematik, hipotesis Riemann merupakan tekaan ahli matematik Bernhard Riemann bahawa semua sifar bagi fungsi zeta Riemann yang bukan disifatkan remeh mempunyai 1/2 sebagai bahagian nyata. Yakni, bagi persamaan ζ(s) = 0 dimana s adalah −2, −4, −6, .... dianggap remeh.
Hipotesis Riemann ialah semua sifar bukan remeh bagi kesinambungan analisis fungsi Riemann zeta mempunyai bahagian nyata 1/2. Keputusan hipotesis Riemann adalah berkaitan dengan taburan nombor perdana. Bukti atau penolakan teori ini akan mempunyai implikasi yang meluas dalam teori nombor, terutamanya untuk pengagihan nombor perdana.
7. Teori Kuantum Yang–Mills
Dalam teori medan kuantum, jurang jisim ialah perbezaan tenaga antara vakum dan keadaan tenaga terendah seterusnya. Tenaga vakum adalah sifar mengikut definisi, dan dengan mengandaikan bahawa semua keadaan tenaga boleh dianggap sebagai zarah dalam gelombang satah, jurang jisim ialah jisim zarah paling ringan.
Teori Kuantum Yang–Mills ialah asas semasa bagi kebanyakan aplikasi teori pemikiran kepada realiti dan potensi realiti fizik zarah asas. Teori tersebut merupakan generalisasi kepada teori elektromagnetisme Maxwell di mana medan kromo-elektromagnet itu sendiri membawa cas.
Kredit: